Decimal codificado en binario
En sistemas de computación, Binary-Coded Decimal (BCD) o Decimal codificado en binario es un estándar para representar números decimales en el sistema binario, en donde cada dígito decimal es codificado con una secuencia de 4 bits. Con esta codificación especial de los dígitos decimales en el sistema binario, se pueden realizar operaciones aritméticas como suma, resta, multiplicación y división de números en representación decimal, sin perder en los cálculos la precisión ni tener las inexactitudes en que normalmente se incurre con las conversiones de decimal a binario puro y de binario puro a decimal. La conversión de los números decimales a BCD y viceversa es muy sencilla, pero los cálculos en BCD se llevan más tiempo y son algo más complicados que con números binarios puros.
Representación BCD
Cada dígito decimal tiene una representación binaria codificada con 4 bits:
Decimal: 0 1 2 3 4 5 6 7 8 9 BCD: 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001
Los números decimales, se codifican en BCD con los bits que representan sus dígitos.
Por ejemplo, la codificación en BCD del número decimal 59237 es:
Decimal: 5 9 2 3 7 BCD: 0101 1001 0010 0011 0111
La representación anterior (en BCD) es diferente de la representación del mismo número decimal en binario puro:
1110011101100101
Fundamentos
En BCD cada cifra que representa un dígito decimal (0, 1,...8 y 9) se representa con su equivalente binario en cuatro bits (nibble o cuarteto) (esto es así porque es el número de bits necesario para representar el nueve, el número más alto que se puede representar en BCD). En la siguiente tabla se muestran los códigos BCD más empleados:
| Decimal | Natural | Aiken | 5 4 2 1 | Exceso 3 |
|---|---|---|---|---|
| 0 | 0000 | 0000 | 0000 | 0011 |
| 1 | 0001 | 0001 | 0001 | 0100 |
| 2 | 0010 | 0010 | 0010 | 0101 |
| 3 | 0011 | 0011 | 0011 | 0110 |
| 4 | 0100 | 0100 | 0100 | 0111 |
| 5 | 0101 | 1011 | 1000 | 1000 |
| 6 | 0110 | 1100 | 1001 | 1001 |
| 7 | 0111 | 1101 | 1010 | 1010 |
| 8 | 1000 | 1110 | 1011 | 1011 |
| 9 | 1001 | 1111 | 1100 | 1100 |
Como se observa, con el BCD sólo se utilizan 10 de las 16 posibles combinaciones que se pueden formar con números de 4 bits, por lo que el sistema pierde capacidad de representación, aunque se facilita la compresión de los números. Esto es porque el BCD sólo se usa para representar cifras, no números en su totalidad. Esto quiere decir que para números de más de una cifra hacen falta dos números BCD.
- Una forma sencilla de calcular números en BCD es sumando normalmente bit a bit, y si el conjunto de 4 bits sobrepasa el número 9, entonces se le suma un 6 (0110) en binario, para poder volver a empezar, como si hiciéramos un módulo al elemento sumante.
Desde que los sistemas informáticos empezaron a almacenar los datos en conjuntos de ocho bits (octeto), hay dos maneras comunes de almacenar los datos BCD:
- Omisión de los cuatro bits más significativos (como sucede en el EBCDIC)
- Almacenamiento de dos datos BCD; es el denominado BCD "empaquetado", en el que también se incluye en primer lugar el signo, por lo general con 1100 para el + y 1101 para el -.
De este modo, el número 127 sería representado como (11110001, 11110010, 11110111) en el EBCDIC o (00010010, 01111100) en el BCD empaquetado.
El BCD sigue siendo ampliamente utilizado para almacenar datos, en aritmética binaria o en electrónica. Los números se pueden mostrar fácilmente en visualizadores de siete segmentos enviando cada cuarteto BCD a un visualizador. La BIOS de un ordenador personal almacena generalmente la fecha y la hora en formato BCD; probablemente por razones históricas se evitó la necesidad de su conversión en ASCII.
La ventaja del código BCD frente a la representación binaria clásica es que no hay límite para el tamaño de un número. Los números que se representan en formato binarioestán generalmente limitados por el número mayor que se pueda representar con 8, 16, 32 o 64 bits. Por el contrario, utilizando BCD, añadir un nuevo dígito sólo implica añadir una nueva secuencia de 4 bits.
Código Gray
¿Qué es el Código Gray?
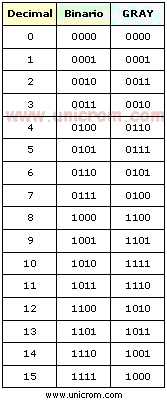
El código Gray es un tipo especial de códigobinario que no es ponderado (los dígitos que componen el código no tienen un peso asignado). Su característica es que entre una combinación de dígitos y la siguiente, sea ésta anterior o posterior, sólo hay una diferencia de un dígito. Por eso también se le llama Código progresivo. Esta progresión sucede también entre la última y la primera combinación. Por eso se le llama también código cíclico. (ver tabla)
El código GRAY es utilizado principalmente en sistemas de posición, ya sea angular o lineal. Sus aplicaciones principales se encuentran en la industria y en robótica. En robótica se utilizan unos discos codificados para dar la información de posición que tiene un eje en particular. Estainformación se da en código GRAY.
Analizando la tabla anterior se observa que:
- Cuando un número binario pasa de: 0111 a 1000 (de 7 a 8 en decimal) o de 1111 a 0000 (de 16 a 0 en decimal) cambian todas las cifras.
- Para el mismo caso pero en código Gray: 0100 a 1100 (de 7 a 8 en decimal) o de 1000 a 0000 (de 16 a 0 en decimal) sólo ha cambiado una cifra.
Código de Exceso 3
El código de exceso 3 se relaciona con el BCD (Ver entrada Código BCD (Código decimal codificado en binario) y algunas veces se utiliza en lugar de éste debido a que posee ventajas en ciertas operaciones aritméticas. Deriva su nombre de exceso 3 debido a que cada grupo de 4 bits equivale al número BCD 8421 mas 3.
El código de exceso 3 para un numero decimal se efectúa de la misma forma que el BCD, excepto que se suma el número 3 a cada dígito decimal antes de codificarlo en binario. Por ejemplo, para codificar el número decimal 4 en código de exceso 3 primero debemos sumar 3 y obtenemos 7. Luego el 7 se codifica en su equivalente binario de 4 bits, 0111.
El código de exceso 3 para un numero decimal se efectúa de la misma forma que el BCD, excepto que se suma el número 3 a cada dígito decimal antes de codificarlo en binario. Por ejemplo, para codificar el número decimal 4 en código de exceso 3 primero debemos sumar 3 y obtenemos 7. Luego el 7 se codifica en su equivalente binario de 4 bits, 0111.
Para poner otro ejemplo convirtamos el número 48 en representación en código de exceso 3:
La tabla siguiente contiene las representaciones en código BCD y de exceso 3 para los dígitos decimales. Nótese que ambos códigos solo emplean 10 de los 16 posibles grupos de códigos de 4 bits. Sin embargo, el código de exceso 3 no usa los mismos grupos de código. Para el código de exceso 3, los grupos de código no válidos son: 0000, 0001, 0010, 1101, 1110 y 1111.


No hay comentarios:
Publicar un comentario